Selasa, 23 Desember 2014

Konsep Sederhana mengenai Hamiltonian

11.32    No comments

Seperti halnya dengan Lagrangian, Hamiltonian juga menjadi solusi di mekanika lanjut. Dimana pada beberapa kasus yang kompleks persamaan geraknya sulit untuk dimanipulasi hanya dengan analisis Hukun Newton saja. Secara sederhana hamiltonian merupakan penjumlahan dari total energi kinetik dari seluruh partikel dan energi potensialnya yang berhubungan dengan sistem. Operator Hamiltonian sering dinotasikan dengan H,  Ȟ dan Ĥ. Secara matematis, bisa dituliskan sebagai berikut :


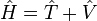
\hat{H} = \hat{T} + \hat{V}

Dimana:

\hat{V} = V = V(\bold{r},t)                                                              (1)
  Yang merupakan operator energi potensial.

        \hat{T} = \frac{\bold{\hat{p}}\cdot\bold{\hat{p}}}{2m} = \frac{\hat{p}^2}{2m} = -\frac{\hbar^2}{2m}\nabla^2                       (2)
Adalah operator energi kinetik, dimana m adalah massa partikel. Dan

\hat{p} = -i\hbar\nabla  adalah operator momentum, dimana ∇ adalah operator gradien. Dot product dari ∇ menghasilkan laplacian ∇2, maka dalam koordinat kartesian 3 dimensi operator laplace menjadi 

\nabla^2 = \frac{\partial^2}{{\partial x}^2} + \frac{\partial^2}{{\partial y}^2} + \frac{\partial^2}{{\partial z}^2}


 Walaupun ini bukan definisi teknis dari Hamiltonian dalam mekanika klasik, bentuk inilah yang sering digunakan. Dengan mengkombinasikan (1) dan (2) maka dihasilkan persamaan yang dikenal dengan persamaaan schrodinger.


                            \begin{align} \hat{H} & = \hat{T} + \hat{V} \\ & = \frac{\bold\hat{p}\cdot\bold\hat{p}}{2m}+ V(\mathbf{r},t) \\ & = -\frac{\hbar^2}{2m}\nabla^2+ V(\mathbf{r},t) \end{align}              (3)

persamaan (3) diatas menunjukkan bahwa Hamiltonian dapat diaplikasikan pada sistem yang dideskripsikan oleh fungsi gelombang . Ini adalah pendekatan yang umum dilakukan sebagai pengantar bagi mekanika quantum.

Partikel Jamak
Pada umumnya banyak partikel dinotasikan sebagai N partikel. Maka Hamiltonian untuk N partikel adalah :

\hat{H} = \sum_{n=1}^N \hat{T}_n + V

dimana

                                 V = V(\bold{r}_1,\bold{r}_2\cdots \bold{r}_N,t)                                               (4)

adalah fungsi energi potensial yang merupakan konfigurasi sistem dan waktu, dan

   ,      \hat{T}_n = \frac{\bold{p}_n\cdot\bold{p}_n}{2m_n}                                    \nabla_n^2 = \frac{\partial^2}{\partial x_n^2} + \frac{\partial^2}{\partial y_n^2} + \frac{\partial^2}{\partial z_n^2} (5)


 adalah operator energi kinetik untuk n partikel. Adapun ∇n adalah gradien untuk partikel ke n, dan ∇n2 adalah laplacian partikel dalam koordinat kartesian.
Mengkombinasikan persamaan (4) dan (5) menghasilkan persamaan Schrodinger Hamilton untuk N keadaan  partikel 


\begin{align} \hat{H} & = \sum_{n=1}^N \hat{T}_n + V \\ & = \sum_{n=1}^N \frac{\bold\hat{p}_n\cdot\bold\hat{p}_n}{2m_n}+ V(\mathbf{r}_1,\mathbf{r}_2\cdots\mathbf{r}_N,t) \\ & = -\frac{\hbar^2}{2}\sum_{n=1}^N \frac{1}{m_n}\nabla_n^2 + V(\mathbf{r}_1,\mathbf{r}_2\cdots\mathbf{r}_N,t) \end{align}


Untuk partikel yang tidak saling berinteraksi dan bergerak bebas, maka potensial dari sistem dinyatakan sebagai separasi energi potensial setiap partikel, sehingga 


V = \sum_{i=1}^N V(\bold{r}_i,t) = V(\bold{r}_1,t) + V(\bold{r}_2,t) + \cdots + V(\bold{r}_N,t)


maka bentuk Hamiltonian yang umum berdasarkan kondisi ini adalah

 \begin{align} \hat{H} & = -\frac{\hbar^2}{2}\sum_{i=1}^{N}\frac{1}{m_i}\nabla_i^2 + \sum_{i=1}^N V_i\\ & = \sum_{i=1}^{N}\left(-\frac{\hbar^2}{2m_i}\nabla_i^2 + V_i \right) \\ & = \sum_{i=1}^{N}\hat{H}_i \\ \end{align}
                                                              (6)


 Persamaan tersebut menyatakan keadaan ideal, pada kenyataanya partikel-partikel dipengaruhi oleh beberapa potensial dan terjadi banyak interaksi antar partikel. Sebagai ilustrasi dimana kondisi pada persamaan (6) diatas tidak berlaku adalah pada potensial elektrostastis. Partikel bermuatan akan berinteraksi dengan partikel lainnya sesuai dengan hukum Coulomb.

Elektrostatis
Energi potensial coulomb untuk muatan titik q1 dan q2 dinyatakan sebagai berikut


                    V = \frac{q_1q_2}{4\pi\epsilon_0 |\bold{r}|}                                                              (7)


persamaan (7) diatas hanya menyatakan potensial satu titik muatan berdasarkan muatan lainnya. Jika terdapat banyak partikel yang bermuatan, setiap partikel bermuatan memiliki energi potensial sendiri terhadap setiap partikel lain yang bermuatan. Untuk N buah muatan, energi potensial dari sebuah muatan qj terhadap seluruh muatan lain adalah


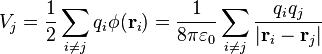
V_j = \frac{1}{2}\sum_{i\neq j} q_i \phi(\mathbf{r}_i)=\frac{1}{8\pi\varepsilon_0}\sum_{i\neq j} \frac{q_iq_j}{|\mathbf{r}_i-\mathbf{r}_j|}


 diamana φ(ri) adalah potensial elektrostatis qj pada ri. Potensial total dari sistem adalah penjumlahan pada seluruh poin j :


V = \frac{1}{8\pi\varepsilon_0}\sum_{j=1}^N\sum_{i\neq j} \frac{q_iq_j}{|\mathbf{r}_i-\mathbf{r}_j|}


 maka diperoleh Hamiltonian sebagai berikut :


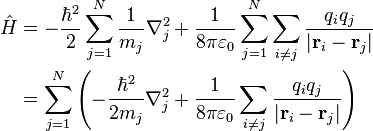
\begin{align}\hat{H} & = -\frac{\hbar^2}{2}\sum_{j=1}^N\frac{1}{m_j}\nabla_j^2 + \frac{1}{8\pi\varepsilon_0}\sum_{j=1}^N\sum_{i\neq j} \frac{q_iq_j}{|\mathbf{r}_i-\mathbf{r}_j|} \\ & = \sum_{j=1}^N \left ( -\frac{\hbar^2}{2m_j}\nabla_j^2 + \frac{1}{8\pi\varepsilon_0}\sum_{i\neq j} \frac{q_iq_j}{|\mathbf{r}_i-\mathbf{r}_j|}\right) \\ \end{align}



 Dipol Listrik dalam Medan Listrik
Untuk momen dipol listrik d berdasarkan muatan sebesar q, dalam medan listrik E yang seragam (tidak gayut waktu), diperoleh potensial :

 V = -\bold{\hat{d}}\cdot\bold{E}

ketika partikel muatan dalam keadaan diam maka tidak ada energi kinetik translasi pada dipol, maka Hamiltonian pada dipol berupa energi potensial

\hat{H} = -\bold{\hat{d}}\cdot\bold{E} = -q\bold{E}\cdot\bold{\hat{r}}


Dipol Magnet dalam Medan Magnet
Untuk momen dipol magnet μ yang diletakkan pada suatu titik dalam medan magnet B yang seragam (tidak gayut waktu) diperoleh potensial

V = -\boldsymbol{\mu}\cdot\bold{B}

ketika partikel dalam keadaan diam maka tidak ada energi kinetik translasi sehingga Hamiltonian dari dipole adalah energi potensial itu sendiri

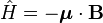
\hat{H} = -\boldsymbol{\mu}\cdot\bold{B}

untuk partikel dengan Spin-½, maka momen magnetik spin adalah


 \boldsymbol{\mu}_S = \frac{g_s e}{2m} \bold{S}
dimana gs adalah spin rasio giromagnetik (spin g-faktor), e adalah muatan elektron, S adalah vektor dari operator spin yang komponennya berupa matrik Pauli. Sehingga diperoleh :


\hat{H} = \frac{g_s e}{2m} \bold{S} \cdot\bold{B}

0 komentar:

Posting Komentar